All Equations You Need to Know for Chemistry 2 Chapters 12-18

NCERT Solutions Grade 9 Maths Chapter 12 – Download Free PDF

NCERT Solutions for Class 9 Maths Chapter 12 – Heron's Formula is provided hither. Heron'south formula is a fundamental concept that finds significance in endless areas and is included in the first term CBSE Syllabus of Grade 9 Maths. Therefore, information technology is imperative to have a clear grasp of the concept. And one of the best means to do but that is past referring to the NCERT Solutions for Form nine Maths Affiliate 12 Heron's Formula. These solutions are designed by knowledgeable teachers with years of experience in accordance with the latest update on CBSE term-wise syllabus 2021-22. The NCERT Solutions for Class nine aim at equipping the students with detailed and step-wise explanations for all the answers to the questions given in the exercises of this Chapter.

Hence, 1 of the best guides you could adapt for your study needs is NCERT Solutions. Relevant topics are presented in an easy to understand format, barring the use of whatever complicated jargons. Furthermore, its content is updated every bit per the last CBSE term-wise syllabus and its guidelines.

Chapter 12-Heron's Formula

Download PDF of NCERT Solutions Course 9 Maths Affiliate 12 Heron's Formula

List of Exercises in NCERTclass 9 Maths Chapter 12:

• Exercise 12.1 Solutions – half dozen Questions
• Do 12.2 Solutions – 9 Questions

Access Answers of NCERT Class 9 Maths Chapter 12 – Heron'south Formula

Exercise: 12.ane (Folio No: 202)

1. A traffic signal board, indicating 'Schoolhouse AHEAD', is an equilateral triangle with side 'a'. Find the area of the signal board, using Heron's formula. If its perimeter is 180 cm, what volition exist the area of the signal board?

Solution:

Given,

Side of the point lath = a

Perimeter of the signal board = 3a = 180 cm

∴ a = threescore cm

Semi perimeter of the signal board (s) = 3a/two

Past using Heron'due south formula,

Surface area of the triangular signal board will be =

2. The triangular side walls of a flyover accept been used for advertisements. The sides of the walls are 122 m, 22 m and 120 m (meet Fig. 12.nine). The advertisements yield an earning of ₹5000 per m² per yr. A company hired one of its walls for iii months. How much rent did it pay?

Solution:

The sides of the triangle ABC are 122 m, 22 m and 120 1000 respectively.

Now, the perimeter will be (122+22+120) = 264 one thousand

Too, the semi perimeter (due south) = 264/2 = 132 one thousand

Using Heron'due south formula,

Surface area of the triangle =

=1320 grandⁱⁱ

We know that the rent of advertising per year = ₹ 5000 per m^two

∴ The rent of one wall for three months = Rs. (1320×5000×3)/12 = Rs. 1650000

3. There is a slide in a park. One of its side walls has been painted in some colour with a bulletin "Keep THE PARK Dark-green AND CLEAN" (see Fig. 12.ten ). If the sides of the wall are 15 thousand, 11 thousand and 6 m, find the area painted in color.

Solution:

It is given that the sides of the wall every bit 15 k, 11 grand and vi m.

So, the semi perimeter of triangular wall (due south) = (15+11+6)/ii m = xvi thousand

Using Heron's formula,

Area of the message =

= √[16(16-15)(xvi-11) (xvi-6)] grand^two

= √[sixteen×one×5×10] m^two = √800 one thousand²

= twenty√ii grand²

4. Find the area of a triangle ii sides of which are eighteen cm and x cm and the perimeter is 42cm.

Solution:

Presume the third side of the triangle to be "ten".

Now, the three sides of the triangle are 18 cm, 10 cm, and "x" cm

Information technology is given that the perimeter of the triangle = 42cm

Then, 10 = 42-(18+10) cm = xiv cm

∴ The semi perimeter of triangle = 42/2 = 21 cm

Using Heron's formula,

Area of the triangle,

=

= √[21(21-18)(21-10)(21-14)] cm²

= √[21×iii×11×7] 1000ⁱⁱ

= 21√eleven cm²

5. Sides of a triangle are in the ratio of 12 : 17 : 25 and its perimeter is 540cm. Observe its expanse.

Solution:

The ratio of the sides of the triangle are given as 12 : 17 : 25

Now, allow the mutual ratio between the sides of the triangle be "ten"

∴ The sides are 12x, 17x and 25x

It is also given that the perimeter of the triangle = 540 cm

12x+17x+25x = 540 cm

54x = 540cm

And so, 10 = 10

Now, the sides of triangle are 120 cm, 170 cm, 250 cm.

So, the semi perimeter of the triangle (s) = 540/ii = 270 cm

Using Heron's formula,

Area of the triangle

= 9000 cm^two

6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Discover the area of the triangle.

Solution:

First, let the third side be x.

Information technology is given that the length of the equal sides is 12 cm and its perimeter is xxx cm.

So, 30 = 12+12+x

∴ The length of the third side = 6 cm

Thus, the semi perimeter of the isosceles triangle (s) = xxx/2 cm = 15 cm

Using Heron'south formula,

Area of the triangle

=

= √[fifteen(15-12)(15-12)(15-six)] cm²

= √[15×3×3×nine] cm²

= 9√fifteen cm²

---

Exercise: 12.2 (Folio No: 206)

1. A park, in the shape of a quadrilateral ABCD, has C = 90°, AB = nine m, BC = 12 thou, CD = 5 m and Advertising = 8 m. How much area does it occupy?

Solution:

First, construct a quadrilateral ABCD and join BD.

Nosotros know that

C = 90°, AB = nine m, BC = 12 m, CD = 5 m and Advertisement = 8 1000

The diagram is:

Now, apply Pythagoras theorem in ΔBCD

BD² = BC² +CD²

⇒ BD² = 12ⁱⁱ+5²

⇒ BD² = 169

⇒ BD = 13 thousand

Now, the surface area of ΔBCD = (½ ×12×five) = 30 m²

The semi perimeter of ΔABD

(s) = (perimeter/2)

= (8+9+thirteen)/ii m

= 30/ii k = 15 m

Using Heron'due south formula,

Area of ΔABD

= 6√35 m² = 35.5 g² (approximately)

∴ The area of quadrilateral ABCD = Area of ΔBCD+Expanse of ΔABD

= 30 mⁱⁱ+35.5mⁱⁱ = 65.5 grand^two

ii. Observe the area of a quadrilateral ABCD in which AB = 3 cm, BC = four cm, CD = 4 cm, DA = 5 cm and Ac = 5 cm.

Solution:

Kickoff, construct a diagram with the given parameter.

Now, use Pythagorean theorem in ΔABC,

Air-conditioning² = AB²+BCⁱⁱ

⇒ 5² = 3ⁱⁱ+4²

⇒ 25 = 25

Thus, it can exist ended that ΔABC is a right angled at B.

So, area of ΔBCD = (½ ×3×four) = 6 cm²

The semi perimeter of ΔACD (due south) = (perimeter/2) = (five+five+4)/two cm = xiv/2 cm = 7 m

Now, using Heron's formula,

Area of ΔACD

= two√21 cm² = 9.17 cm² (approximately)

Area of quadrilateral ABCD = Area of ΔABC + Area of ΔACD = vi cm² +9.17 cmⁱⁱ = 15.17 cm²

3. Radha made a picture show of an aeroplane with coloured paper as shown in Fig 12.15. Find the total area of the paper used.

Solution:

For the triangle I section:

It is an isosceles triangle and the sides are v cm, 1 cm and 5 cm

Perimeter = 5+five+1 = 11 cm

And then, semi perimeter = 11/2 cm = five.5 cm

Using Heron's formula,

Expanse = √[s(s-a)(due south-b)(due south-c)]

= √[five.5(five.five- 5)(5.5-5)(5.5-i)] cm^two

= √[v.5×0.v×0.5×4.v] cm²

= 0.75√11 cm^two

= 0.75 × three.317cm²

= 2.488cm² (approx)

For the quadrilateral II section:

This quadrilateral is a rectangle with length and breadth as six.5 cm and 1 cm respectively.

∴ Area = six.5×1 cm²=vi.5 cm²

For the quadrilateral 3 section:

It is a trapezoid with 2 sides as one cm each and the third side as 2 cm.

Expanse of the trapezoid = Expanse of the parallelogram + Surface area of the equilateral triangle

The perpendicular height of the parallelogram volition exist

= 0.86 cm

And, the area of the equilateral triangle will exist (√iii/four×aⁱⁱ) = 0.43

∴ Area of the trapezoid = 0.86+0.43 = 1.3 cm² (approximately).

For triangle IV and Five:

These triangles are 2 congruent correct angled triangles having the base equally 6 cm and summit 1.5 cm

Area triangles Iv and V = 2×(½×half-dozen×one.5) cm² = 9 cm²

And then, the full area of the paper used = (2.488+6.5+1.iii+9) cm² = nineteen.3 cmⁱⁱ

4. A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, detect the top of the parallelogram.

Solution:

Given,

Information technology is given that the parallelogram and triangle take equal areas.

The sides of the triangle are given as 26 cm, 28 cm and thirty cm.

So, the perimeter = 26+28+30 = 84 cm

And its semi perimeter = 84/2 cm = 42 cm

Now, by using Heron'south formula, area of the triangle =

= √[42(42-26)(42-28)(42-30)] cm²

= √[42×16×fourteen×12] cm²

= 336 cm^two

At present, let the height of parallelogram exist h.

As the area of parallelogram = area of the triangle,

28 cm× h = 336 cm²

∴ h = 336/28 cm

And then, the top of the parallelogram is 12 cm.

5. A rhomb shaped field has dark-green grass for xviii cows to graze. If each side of the rhombus is 30 one thousand and its longer diagonal is 48 m, how much expanse of grass field volition each cow be getting?

Solution:

Draw a rhombus-shaped field start with the vertices equally ABCD. The diagonal AC divides the rhombus into ii congruent triangles which are having equal areas. The diagram is as follows.

Consider the triangle BCD,

Its semi-perimeter = (48 + 30 + 30)/2 m = 54 m

Using Heron'southward formula,

Area of the ΔBCD =

= 432 thou²

∴ Area of field = 2 × area of the ΔBCD = (2 × 432) yard^two = 864 yard²

Thus, the expanse of the grass field that each moo-cow will be getting = (864/18) thousand^two = 48 thou²

six. An umbrella is fabricated by stitching 10 triangular pieces of cloth of ii different colours (see Fig.12.16), each piece measuring 20 cm, 50 cm and 50 cm. How much textile of each color is required for the umbrella?

Solution:

For each triangular piece, The semi perimeter will be

s = (50+l+xx)/2 cm = 120/ii cm = 60cm

Using Heron's formula,

Expanse of the triangular piece

=

= √[60(lx-50)(60-50)(60-20)] cm²

= √[60×10×10×twoscore] cm^two

= 200√6 cm^two

∴ The expanse of all the triangular pieces = 5 × 200√6 cm² = 1000√6 cm²

7. A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and sides half dozen cm each is to exist fabricated of three different shades every bit shown in Fig. 12.17. How much newspaper of each shade has been used in information technology?

Solution:

As the kite is in the shape of a square, its area will exist

A = (½)×(diagonal)²

Area of the kite = (½)×32×32 = 512 cm^2.

The expanse of shade I = Expanse of shade 2

512/2 cm^two = 256 cm²

So, the total area of the paper that is required in each shade = 256 cm²

For the triangle section (III),

The sides are given as half dozen cm, half dozen cm and eight cm

Now, the semi perimeter of this isosceles triangle = (6+6+8)/two cm = 10 cm

By using Heron's formula, the area of the III triangular piece volition be

=

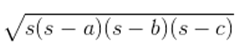
= √[x(10-6)(x-6)(10-viii)] cmⁱⁱ

= √(10×4 ×4×2) cmⁱⁱ

= 8√5 cmⁱⁱ = 17.92 cm² (approx.)

viii. A floral design on a floor is made up of xvi tiles which are triangular, the sides of the triangle being ix cm, 28 cm and 35 cm (see Fig. 12.18). Find the cost of polishing the tiles at the charge per unit of 50p per cm² .

Solution:

The semi perimeter of the each triangular shape = (28+9+35)/ii cm = 36 cm

Past using Heron's formula,

The area of each triangular shape volition be

= 36√half-dozen cm^two = 88.2 cm²

Now, the total expanse of xvi tiles = 16×88.2 cm² = 1411.2 cmⁱⁱ

It is given that the polishing price of tiles = l paise/cm²

∴ The full polishing toll of the tiles = Rs. (1411.2×0.v) = Rs. 705.6

9. A field is in the shape of a trapezium whose parallel sides are 25 m and 10 grand. The non-parallel sides are 14 m and 13 1000. Find the surface area of the field.

Solution:

Outset, describe a line segment Exist parallel to the line Ad. Then, from B, draw a perpendicular on the line segment CD.

Now, it can be seen that the quadrilateral ABED is a parallelogram. So,

AB = ED = 10 m

AD = Be = 13 1000

EC = 25-ED = 25-10 = 15 m

Now, consider the triangle BEC,

Its semi perimeter (s) = (13+xiv+fifteen)/2 = 21 grand

By using Heron's formula,

Area of ΔBEC =

= 84 yard²

We also know that the area of ΔBEC = (½)×CE×BF

84 cm² = (½)×fifteen×BF

BF = (168/xv) cm = eleven.2 cm

And so, the total surface area of ABED will be BF×DE i.due east. 11.2×x = 112 m²

∴ Area of the field = 84+112 = 196 m²

---

Affiliate 12 Heron'south Formula belongs to Unit 5: Mensuration. This unit carries a full of 13 marks out of 100. Therefore, this is an of import affiliate and should exist studied thoroughly. The important topics that are covered under this chapter are:

• Area of a Triangle – past Heron's Formula
• Awarding of Heron's Formula in finding Areas of Quadrilaterals

Heron'south formula helps usa to find the expanse of a triangle with 3 side lengths. Besides the formula, Heron also contributed in other ways – the most notable ane being the inventor of the very first steam engine called the Aeolipile. Withal, Heron couldn't notice any applied applications for it, instead, it concluded upward beingness used as a toy and an object of marvel for the aboriginal Greeks.

Explore more about Heron'southward Formula and learn how to solve various kinds of bug simply on NCERT Solutions For Grade 9 Maths. It is also i of the best academic resources to revise for your first term exams.

Key Features of NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula

1. Well-structured content
2. Relevant formulas are highlighted
3. Easy-to-understand language and jargon-free explanations
4. Designed by qualified teachers
5. Latest questions with solutions from the updated term-wise syllabus
6. A thorough analysis of previous year question papers
7. Access to other learning resources such as sample papers and more than

The good kinesthesia team of members have formulated the solutions in a lucid manner to improve the trouble-solving abilities amidst the students. For a more articulate idea about Heron'south Formula, students can refer to the study materials bachelor at BYJU'S.

• RD Sharma Solutions for Class ix Maths Affiliate 12 – Heron's Formula

Frequently Asked Questions on NCERT Solutions for Class nine Maths Chapter 12

What is the main aim of NCERT Solutions for Class ix Maths Chapter 12?

The students are encouraged to go through NCERT Solutions for Grade nine Maths Chapter 12 thoroughly before the beginning term exams to score well and intensify their trouble-solving abilities. Agreement the concepts and clearing the doubts immediately during self-written report is the master aim of these solutions.

What are the primal benefits of learning NCERT Solutions for Class 9 Maths Affiliate 12?

Key benefits of NCERT Solutions for Class 9 Maths Affiliate 12 are provided here:
1. Students can easily access the solutions for each do from the chapters available.
2. The solutions also provide graphs and illustrations that aid to understand the concepts clearly.
3. These solutions are prepared by BYJU'Southward skillful team focussing on accuracy.

Why should nosotros refer to NCERT Solutions for Class 9 Maths Chapter 12?

Students can refer to these NCERT Solutions for Class ix Maths Affiliate 12 which helps in gaining knowledge and for better guidance its best to solve these solutions. Solving these exercises in this chapter will assure that students can score good marks in the first term exams.

All Equations You Need to Know for Chemistry 2 Chapters 12-18

Source: https://byjus.com/ncert-solutions-class-9-maths/chapter-12-herons-formula/

Share this post